Of course times t₁ and t must have the same units (i.e., either seconds, minutes, etc.). Intuitively one might expect a for metals to vary drastically according to the surface conditions of the metal. This usually isn't the case. For example, Schram reported an a for anodized aluminum - a metal sponge, if ever there is one - of 0.9, whereas for unbaked aluminum he reported an a of 1.0.¹ However, q₁ for the anodized aluminum is ~ 44 times greater than that of the fresh or unbaked aluminum.
The total system outgassing rate is just A x q_m (t), where A is the material surface area . The value A x q_m (t) divided by the system pump speed, S, near the vacuum gauge, yields P_m (t), the system pressure as a function of time. Therefore, (1) can be modified accordingly:

equation (2).

P_m (t) = P₁ x (t / t₁)^{- a}

By now you must be wondering what this all means. It means just this: assume that the "free" gas in the vacuum system is pumped away comparatively quickly, and it's an all-metal system. The chamber pumpdown pressure as a function of time, if plotted on log-log paper, will yield a slope of pressure v. time of approx. -1. On the other hand, if the system has just a few elastomer sealed components, only after an extended time, will a pressure v. time slope of -0.5 to -0.6 be observed. If the system has a large number of o-rings, the outgassing from the metal will be in the noise, and the pumpdown slope will be -0.5 to -0.6 throughout time.
We are able to deduce this by taking the log of both sides of (2) and solving for the value of a. That is,

equation (3).

[log P_m (t) - log P₁] ¸ [log t - log t₁] = - a

Let's take a look at some examples. Assume that you have an all-metal system with a total surface area, A ~ 2 x 10⁴ cm², and that the H₂O pump speed delivered to the chamber is ~ 3300 L/s. Figure 1 shows a calculated plot of system pressure v. time on log-log paper for chambers constructed of both clean and anodized (i.e., dirty) aluminum. Note that the initial slopes of both pumpdown curves are approximately -1. The pumpdown curve for the clean aluminum asymptotes at ~10^{- 8} torr. This is because it was assumed that the blank-off pressure of the pump (i.e., the ultimate or base pressure) was ~10^{- 8} torr. Though the initial slopes of the two curves are almost the same, the difference in calculated system pressures for the same time differ by the factor of ~44 previously discussed. Using the values of speed and surface area given in the figure, the reader should be able to calculate an approximate value of q₁ for both types of aluminum.

O-Ring Sealed System

"But Kimo, I've got a system with both metal surfaces and elastomer seals." No problem; the pumpdown curve will merely be the algebraic sum (i.e., linear superposition) of the pressure due to the elastomer outgassing in time and the pressure due to metal surfaces outgassing in time.
De Csernatony showed that the equivalent outgassing surface area of an o-ring in a groove comprises half of the total area of the o-rings.⁶ On doing an inventory of the equivalent amount of Viton used in the manufacturer's system, I was shocked to find that it totaled ~2750 cm². That is, the surface area of o-rings in their systems totaled >10% of the system's metal surfaces!
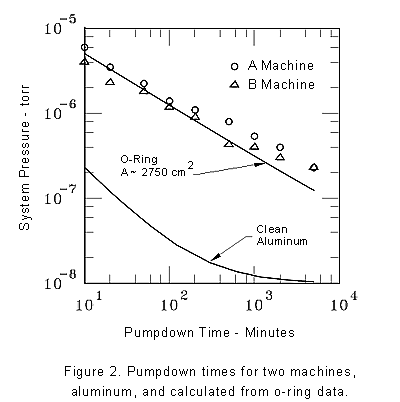
To clearly demonstrate to the manufacturer the source of the problem, I plotted: i) actual system pumpdown rates; ii) the theoretical pumpdown curve for Viton using reported data;⁴ and, iii) the pumpdown rate to be expected for clean aluminum, all assuming a 3,300 L/s pump speed. These findings are summarized in Fig. 2. Note that though a's for the systems were ~0.49, and ~0.59 for calculated pressure values based on the Viton data, the pressure magnitudes tracked closely. Again, the outgassing due to the clean aluminum chamber was negligible.

Needless to say, the manufacturer was very displeased with the findings. I suspect that they knew what the problem was when I walked in the door, but were hoping for a silver bullet cure. They asked if there was some manner in which they might treat the o-rings to reduce the outgassing? This is no help, for it has been shown that the sorption of air gasses and water vapor in o-rings is a completely reversible process 24 hours after venting a vacuum system to air.⁴

Predicting System Outgassing

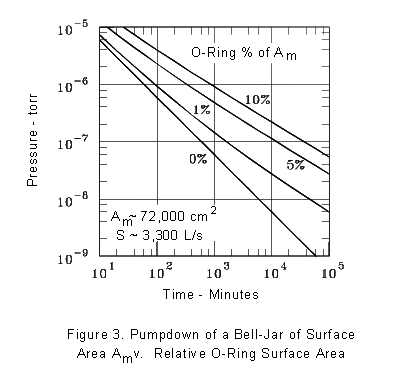
Using the simple models described it is possible to fairly accurately predict system pumpdown pressure in time for any o-ring sealed, metal system. Figure 3 illustrates what is to be expected when pumping down a 270 L bell-jar. The bell-jar has clean, internal sputter-shields which have the effect of increasing the internal metal surface area of the bell-jar, A_m, by a factor of three. It was assumed that the blank-off pressure of the pump for water vapor was 10 ^{- 11} torr. This is not unreasonable for a cryopump. Also, if a cross-over pressure of ~0.1 torr is used, and a cryopump air speed of 1,200 L/s assumed, the air gases in the system will be removed in seconds.

If you lay a straightedge along side of the 1% and 5% data, you will see that they curve, and that their slopes are decreasing in time. This is because the dominant source of outgassing in time is becoming that of the o-rings. The 10% data are almost totally dominated by o-ring outgassing.

Conclusions

4 Analysis of the slopes of vacuum system pumpdown curves can be very instructive.
4 The blank-off pressure of the pumps must be considered in the slope analysis.
4 One can accurately predict the effect o-rings have on system pumpdown times.
4 The sorption of air gases in o-rings is a completely reversible process.
4 What price o-rings? Just time!

Reference

1 Ishimaru, H., J. Vac. Sci. Technol. A7 (3), 2439 (1989).
2 O'Hanlon, J.F., A User's Guide to Vacuum Technology, 2nd Ed. (John Wiley & Sons, New York, 1989), p. 445.
3 A registered trademark of E.I. du Pont Nemours and Company.
4 Welch, K.M, McIntyre, G., Tuozzolo, J.T., et al, Vacuum 42 (7-9), 1924 (1990).
5 Schram, A., LeVide No 103, 58 (1963).
6 de Csernatony, L., Crowley, D.J., Vacuum 17 (10) ,551 (1967).

© Copyright Kimo M. Welch February 2000.