|
|
 |
|
Printable
version of this article in Adobe Acrobat Format
|
Finger Pointing in the
Fab ©
Introduction
The general public looks at vacuum as the absence of all matter.
The hatch on the spaceship bursts open and the alien monster is
sucked out, spinning off into nothingness. We can no longer hear
an alarm clock ringing in the bell jar when it is evacuated with
a mechanical pump. We conclude that this is because there is nothing
left in the bell jar to conduct sound. We are greeted in the elevator
of a hotel convention center with the tiring joke: "Ahah,
much ado about nothing," when they see on our name tag the
American Vacuum Society, or the Society of Vacuum Coaters. To
the contrary, vacuum has much to do with our every day lives.
But, the story is too lengthy to explain on the elevator.
|
|
A Little Mathematics Tells a Lot
The story of what is going on in a vacuum system starts with the
basic equation of state first encountered in high school or freshman
chemistry:
where
|
|
PV =
|
n RT, (1)
|
|
P =
|
the pressure in torr,
|
|
V =
|
the volume in liters,
|
|
n =
|
the number of moles,
|
|
T =
|
the temperature in degrees kelvin,
|
|
R =
|
the universal gas constant,
|
|
and
A mole of anything is 6.02 x 1023 of those things (i.e.,
boxcars, atoms, molecules, etc.). The universal gas constant R varies
depending on the other units. This sounds like an oxymoron - that
is, to say a constant varies depending ... But, we vacuum technicians
have made a jumbled mess of the units of pressure, and the value
of R varies depending on the unit of pressure used. Chemists use
the unit atmospheres; physicists Pascal (newtons per
square meter); Europeans adopted the millibar; engineers,
pounds per square inch (psi); and, others mystified their
work for decades using mmHg for the unit of pressure, and
later changed this to torr.
|
|
Seeing the error of our ways, we all took a blood oath in the late
1980s, and swore to hence forth universally adopt the pressure unit
of Pascal (Pa). Well, with the exception of the Japanese and others
on the Pacific Rim, the world drifted back to its old habits. USA
publications presently use the unit torr, with Pascal given parenthetically;
Europeans almost exclusively use millibar; and, of course, we could
never hope to change the chemists and engineers. It is suggested
that before our children and grandchildren get a feel for torr,
we start using the mks unit Pascal for pressure. However, if you,
like us old-timers, have trouble changing, the universal gas constant
when using the unit torr for pressure is (please keep out of the
reach of children):
|
|
R = 62.36 torr-liters/mole-degree K.
|
So what, Kimo? Well, if you were to take a snapshot of what's going
on in your vacuum system at any instant in time, you can actually
count the number of molecules in the system using (1). Also, if the
pressure in the vacuum system is ~10 -6 torr, molecules
are impinging on every surface in that system at a rate of ~10
15 molecules/cm2-sec. If all the molecules stuck
to the surfaces, this would correspond to a monolayer build-up each
second. Of course, they don't necessarily stick when they hit the
surface, but they bombard the surface at that rate. Why is this important?
Well, if the impinging molecules are chemically reactive with the
surface, the surface may not have the chemical makeup you originally
intended due to the reactions (e.g., "cloudy" films, etc.).
So the idea that there is nothing in the bell jar because we can't
hear the alarm clock is nonsense. Processes going on in a vacuum
system are dynamic and very active at even ulta-high vacuums (i.e.,
£ 10 -9 torr).
|
Massaging Equation 1
Things become a little more interesting when we differentiate (1)
with respect to time. Doing so, we obtain:
|
|
PDV/Dt + VDP/Dt = D(nRT)/Dt
(2)
|
What the basic equation F = ma is to the physicist, (2) is of similar
importance to we vacuum technicians. The term DV/D
t in (2) is given the symbol S, for speed. Pump speed
might correspond to some chemisorption process when growing films
in the chamber, to pumping on the chamber with some form of vacuum
pump, or both. The term on the right of (2) is given the symbol Qo.
It is called the total throughput into the system. The total throughput
may comprise any or all of: i) leaks into the system; ii) outgassing
from surfaces; iii) diffusion of gas into the system; iv) gases introduced
to create some process (e.g., CVD, PVD, etc.) in the system; or, v)
gas byproducts created by a process.
We will come back to this equation numerous times in subsequent
columns. But, for now, let's examine (2) assuming that the only
source of throughput into the room-temperature system is a leak.
Equation. 2 then takes the form:
|
|
PS + VDP/Dt = Qo (3)
|
Assume that we are leak checking the system, and that we spray helium
on the leak at time t = 0. Solution of (3) takes the form:
|
P(t) = (Qo/S) x (1
- e -St/V) (4)
|
That is, the helium partial pressure in the chamber as a function
of time, P(t), rises in direct proportion to the leak rate into the
chamber, and is inversely proportional to the size of the pump pumping
on the chamber. This finding may contradict the conventional wisdom
of most who have poked around a vacuum system trying to find a leak.
The value of S is of course the effective speed delivered to the chamber
through various interposed conductances between pump and chamber.
Examination of (4) leads us to some logical conclusions. First,
we know there are competing processes going on. A large volume,
V, suggests that it will take a longer time before the helium pressure
from the leak equilibrates in the volume, as there is much to fill,
and the pump is pumping away some of the in-leaking gas. Secondly,
it is obvious that the greater the leak, Qo,
the greater the leak signal in time (i.e., P(t)) in the chamber.
We also see the trade-off of sensitivity v. response time in (4).
It would be most instructive to the reader to enter the variables
on a spreadsheet, and calculate response times, signal levels, etc.,
as a function of these variables. Let's go on to a more difficult
problem; that is, determining if system difficulties in fact stem
from some leak.
A Little Logic Goes a Long Way
Assume that we work in some fab, and that folks are arguing about
why a system won't pump down (i.e., who did what and when). Rather
than some fancy cluster tool system, it is simply a batch coater,
with a 1,000 L volume, and planetary tooling such as shown in Fig.
1. The system today is basing out at a pressure of ~2 x 10
-6 torr. The problem is that, though we don't keep system
performance records (ugh), we recall that yesterday the system based
out at ~2 x 10 -7 torr.
|
|
|
Last night the Production people put new tooling in the bell-jar.
Also, the Maintenance people switched compressors on the cryopump.
The compressor was due to have the adsorber changed. The maintenance
people thoroughly leak checked the system today and found no leaks.
They were able to valve-off the high vacuum pump when leak checking,
so as to have the best possible sensitivity (i.e., see (4)). Also,
the temperatures of the cryopump's first and second stages look OK.
The maintenance people say: "The tooling is dirty or has
a virtual leak." The Production people say: "The
tooling if OK, but the Maintenance screwed up the pump."
Formal logic has it that if one makes an assumption, legitimately
tests the assumption, and reaches a contradiction, then the original
assumption is proven wrong. As a trivial example, assume that we
have nine (9) apples in a bowl. Claim that the apples weigh on average
at least 0.25 pounds each. (This is your assumption.) You put the
apples in a paper bag, measure their combined weight, and find it
to be 2.1 pounds. (This is a legitimate measurement.) Next you divide
the total measured weight by the number of apples to get the average
weight. (This is a legitimate calculation.) The measurement and
calculation indicates that the apples weigh on average ~0.23 pounds.
This contradicts your original assumption. Therefore, your original
assumption is incorrect.
Let's use the same technique to diagnose the above system problem.
Assume that the speed of the pump, Sp is 1,500
L/s. This is based on the manufacturer's data sheet, and is probably
correct, if the pump is not defective, to within ± 20%. Calculate
the effective speed delivered to the bell-jar, Se, assuming an interposed
conductance of C. The method of doing this can be found in any one
of a dozen vacuum handbooks. 1-3
Say the results of your (legitimate) calculation suggests a value
of Se of 1,000 L/s. We can now go back to (3),
and plug in the value of P x Se in that equation.
Note also, the system has been pumped on overnight, and therefore
the pressure is not changing in time. This means that the second
term in the left part of (3) is zero. That is, V x DP/D
t º 0. Then, (3)
takes the form:
|
|
P x Se = Q1o (5)
|
|
or, (2 x 10 -6torr) x 1000 L/s = 2
x 10 -3 torr - L/s
|
You've taken the measured pressure, and multiplied it times the calculated
speed, and come up with an implied throughput, Q 1o, into
the system. Don't worry about possible errors in gauge calibration
just yet.
|
 |
|
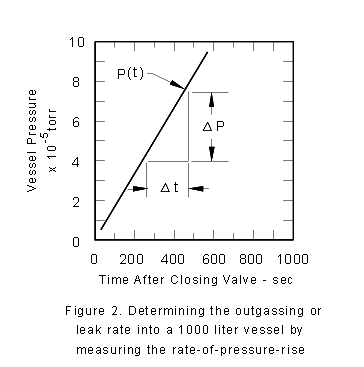
Now, let's close the high vacuum valve at the pump inlet. This results
in the pressure rising in time. In fact, returning to (3), we determine
that the volume of the system times the rate at which the pressure
rises is just another means of determining Q. Note that by closing
the high vacuum valve you have forced Se in (3)
to become zero. You monitor pressure as a function of time in the
valved-off bell-jar, and plot the results of this (legitimate) measurement
in Fig. 2. The pressure rises at a rate of 10 -4 torr/600s.
That is
|
V x DP/Dt = Q2o
(6)
|
|
or, 1,000 L x 10 -4 torr/600s = 1.7
x 10 -4 torr - L/s ®¬
|
|
The symbol "®¬
" means you have reached a contradiction. Note that
you have used the same gauge to make the rate-of-pressure rise measurement
as was used to previously measure the based-out pressure of the
system. Therefore, gauge calibration is not an issue. Also the results
when plugging the numbers into (5) and (6) contradict each other
by more than a factor of ten (10).
The results of all of your calculations might cause a disparity
in the two results of perhaps 30%-40%, but not 1,000%. Therefore,
this can mean only one thing: your original assumption about the
effective speed delivered to the bell-jar, Se, being
1,000 L/s, was erroneous. This finding can result from only two
possibilities: i) the pump is defective; or, ii) there is some obstruction
between the bell-jar and pump.
What if the results of the two calculations agreed to within 30%-40%?
This would mean that the pump is not defective, there is no obstruction
between the pump and chamber, and there is probably a virtual leak
somewhere in the system.
The power of this simple analytical tool often escapes even those
who manufacture systems. By your use of this logic you have been
led to an obvious result, and thus eliminated finger pointing in
the fab.
On publication of this article in the magazine Vacuum Technology
& Coating, I was critiqued by a friend and colleague Phil Lessard.
Phil pointed out that if there is a lot of surface pumping in the
vacuum system, or the "leak" into the system happens to
be water vapor, the pressure rise may not be linear in time. This
is a most important comment. Indeed, we must be wary of any pat
solutions when diagnosing system problems. Thanks, Phil, for the
comment.
Reference
1 John F. O'Hanlon, A User's Guide to Vacuum Technology,
2nd Ed. (John Wiley & Sons, New York, 1989).
2 Marsbed H. Hablanian, High-Vacuum Technology, A Practical
Guide, 2nd Ed. (Marcel Decker, Inc., New York, 1997).
3 Kimo M. Welch, Capture Pumping Technology, 2nd Edition
(Elsevier Science, Amsterdam, 2001).
© Copyright Kimo M. Welch February 2000.
|
|

